Measuring the Distance to the Sun with the Transit of Venus

With the upcoming transit of Venus, scientists from across the world are coordinating with groups to measure the contact times of the transit and re-measure the distance to the Sun. There are several websites (such as this one, or this one) that detail how to do this, and a nice (math heavy) paper by Mignard in 2004 (PDF file here). Many of these methods, however, require you to get the full duration of the transit or directly measure the parallax with imaging. Here I describe a much more simple method that requires you to measure only the time at ingress interior or egress interior for two locations on the Earth. This method is convenient as you don't need to witness the full transit (only ingress seen from Easter Island, for example). This is a retelling of the information derived by Udo Backhaus in this website with some added explanations.


Wait, what's ingress interior?
This is best explained with a diagram:

Above, you can see the path that Venus will take across the Sun (in the equatorial view). There are four contact points of note: first contact, when Venus just touches the disk of the Sun; second contact, when Venus is fully inside the solar disk; third contact, when Venus is just about to leave the disk; and fourth contact, when Venus has just left the disk of the Sun.
There are more technical term for these contact times. The first two contact points are ingress because Venus is moving into the solar disk, likewise the two later points are egress because Venus is leaving it.
The outer most points are exterior points (ingress exterior/egress exterior) and the inner ones are, not surprisingly, interior points.

When I refer to ingress interior I am talking about the second contact point. Egress interior is the third contact point. This method relies on accurately measuring the time when either of these take place.


Now, the Math
In order to understand how we go about measuring the distance to the Sun, we need to go over some math. This is just basic geometry and algebra. If you'd rather just skip to the answer, scroll down to the "Wrapping it all up" section.

Imagine a giant circle of radius D and a small arc of it (s) along its edge. As can be seen below, this arc subtends an angle θ:

Mathematically, this can be expressed as s = θD. In other words, if you know the length s and the angle θ you can calculate what the distance D is. This works for velocities as well: v = ωD, where ω is an angular speed.
These simple geometric concepts form the basis for this method.

Consider the motion of the Earth as it moves into the shadow of Venus as seen from the Sun. At ingress exterior, the Earth is just touching the shadow and we see Venus just hitting the Sun's disk. At ingress interior, the Earth has fully moved into the shadow and the transit is well underway. It should come as no surprise, that in that time the Earth has moved one full Earth diameter (2 Earth radii: 2*R_E). Hence we have:

2 R_E = D θ

with D now being the distance between the Sun and the Earth.
The angle θ can be a bit troublesome to measure, so instead let's rely on the angular motion and the amount of time (Δt) between ingress exterior and interior:

2 R_E = D ω Δt    or in other words: D = 2 R_E / Δt  * 1/ω

If we can measure the time Δt we can estimate the distance to the Sun since we already know the radius of the Earth and the angular speed.

Now, about the angular speed: what we need is not just Earth's angular speed, but the relative speed between Venus and the Earth (since both are moving). We know how long a year is for both planets and this corresponds to the amount of time for them to cover a full circle, or 2π radians. Hence, the angular speed for a planet will just be ω = 2π / P, where P is the period (the length of the year).
For Venus, this is 3.2364E-7 per second, and for Earth, 1.992E-7 per second. I'm using scientific notation here so 1E2 = 1*10^2 = 100 and 1E-2=1*10^(-2)=0.01.
The relative angular motion that we need is then the difference: 1.244E-7 per second.
Note that in practice the orbits aren't perfect circles, but this is good enough for our purposes. We'll come back to that later.


A correction factor
The relationship above would be perfect if the Earth enters the shadow of Venus through the center. Alas, it does not and we need to account for this difference. This is done by measuring the 'impact parameter' (p) of the path of the Earth through Venus's shadow:

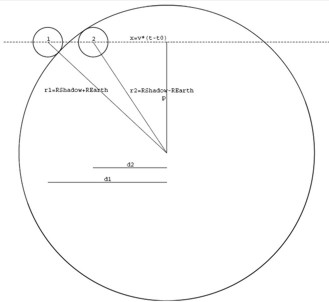Note that in this figure, the small circle is the Earth at the first and second contact times and the large circle is the shadow of Venus at Earth's distance.

The figure above has labels for all the quantities of interest. The variable r corresponds to the true separation between the center of the shadow and the center of the Earth while d corresponds to the horizontal projection of this distance. The variable p is the vertical separation between the path of the Earth and the center of Venus's shadow. Since these are right triangles, the following holds:

r^2 = p^2 + d^2

The distance r1, for example, is just the sum of the radius of the shadow (R_S) and the radius of the Earth (R_E), whereas r2 is the difference between these two quantities.
Also, recall from above that when the Earth fully enters the shadow it has moved a horizontal distance 2*R_E. This can be expressed more generally as:

d1 - d2 = v Δt'

where v is the velocity (v = ωD) and Δt' is the time between event 1 and 2.
We can combine the relationships as follows:

Now we can make use of all of these and place them together:

That last line should look very familiar as it's the same relationship we had before but with an extra factor thrown in. The value of p depends on the parameters of the event. As mentioned here, the value for the June 5, 2012 transit of Venus is 0.5904 R_S and thus the correction factor is 1.23899.


The final bit
We're now ready for the last part. The gist of it is again very simple: the velocity the Earth takes across the shadow is a constant v and is given by 2 R_E / Δt. Since this is a constant, we can measure that using any two arbitrary positions separated by Δx: v = Δx / Δt'
Hence, we can rewrite our full expression as:

In this context, x is the horizontal distance separating two points as the shadow moves across them. Unfortunately, this is not just a straightforward comparison of the latitude and longitude. Here's what we're dealing with:

The shadow of Venus is moving from right to left in this diagram and the vertical grey lines correspond to constant x.
Calculating x given latitude and longitude is straightforward, but the derivation behind it is not so I skip that (but you can see a discussion here). Here's what you need to use given latitude (ϕ) and longitude (λ):

We now have every relationship we need to get the distance, so let's wrap it all up and work out an example.


Wrapping it all up
To calculate the distance to the Sun we use the following relationship:

We know most of the numbers for this, so I'll just put them in:

The separation Δx can be calculated with this relationship using the latitude (ϕ) and longitude (λ) at two sites:

The time Δt is just the time difference, in seconds, between ingress interior or egress interior measured at two locations.


An example
Let's consider observers at Hanga Roa, Easter Island and Maui, Hawaii.
The latitude, longitude, and expected contact times are as follows:

Location	Latitude	Longitude	Contact Time
Easter Island	-27.150	-109.4333	22:28:18
Hawaii	20.79836	-156.33193	22:27:38

The x distances for these two locations are 0.03 and 0.12 Earth radii, respectively.
Note that these two are effectively very closely spaced and thus the transit starts at nearly the same time. The difference between contact times reflects this: Δt is just 40 seconds. Two observers separated an Earth radius apart in x would have seen a difference of about 7 minutes. Hence, combining Hawaii and Easter Island may not be the best choice, but it still works as long as we have a precise measurement.

Putting it all together, we see that Δx/Δt is 0.00231 Earth radii/second and thus the distance to the Sun is 23,002 Earth radii. The radius of the Earth is 6367.5 km, so that corresponds to a distance of 146 million kilometers.

The astronomical unit (AU) is 150 million kilometers. Hence, the distance we have measured is 0.9791 AU. But WAIT! It turns out that the distance between the Earth and the Sun varies since the orbit is not a perfect circle. Using the fantastic WolframAlpha website, we can see that on that date, the separation between the Earth and the Sun is actually 1.015 AU.
The difference between our estimate and the true value is only 4% --- not bad!

A final note: you can use more than two locations for this. In that instance, you would plot x as a function of Δt and fit a straight line to estimate the slope (m=Δx/Δt).


How YOU can get involved
This procedure is relatively straightforward and we intend to apply it to the contact times that school groups in Easter Island measure. We already have several teams across the globe that will provide additional contact times at separate locations. If your school or a group you know want to get involved, let us know through this page. The more measurements of the contact time we get, the better we can do this!

More information on the Easter Island Venus Transit event can be found here.

UPDATE: July 19, 2012

I wanted to mention 3 things:

1- I had forgotten to reference that this method is that of the French astronomer Joseph-Nicolas Delisle. It was developed in 1753 for the observation of the transit of Mercury.

2- Through complete oversight, I didn't realize or note that 'x' varies as a function of time since the Earth rotates and the position of Venus and the Sun changes. Hence, the 'x' formula I provide above is valid only for 1st and 2nd contact. For 3rd or 4th contact, you need to use:

3- And finally, we have successfully applied this for the 2012 transit of Venus. School and outreach teams from across the world joined us in measuring the contact times and we calculated a value of 151+/-20 million kilometers for the distance to the Sun. The details on what we did are described here.